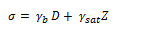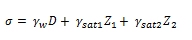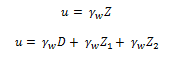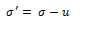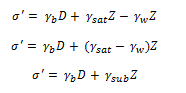The Structural loads are supported on soil through foundations. These loads produce stresses and resulting strains or deformations in the soil below the foundation. The deformation in the vertical direction is usually termed as settlement, which occurs due to the vertical stresses.
 |
| Stresses in a Soil Mass |
The stresses which produce excessive deformations are termed as failure stresses.
Geostatic Stress or Over Burden Pressure
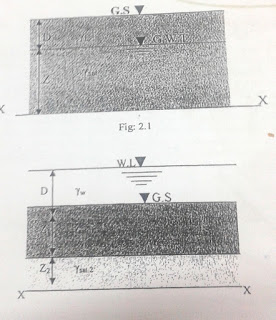
At any point within soil mass, stresses are also developed due to the soil layer above that point, known as geostatic stress or over burden pressure. The magnitude of geostatic stress at a point is affected by the groundwater table fluctuation above that point.
The intensity of stress developed is not uniform but vary from point to point. For the design of structure such as retaining walls, sheet piles for braced excavations and water front structures and some types of pile foundations, stress acting in the horizontal direction are more important.
The knowledge of stress distribution along a soil cross-section is important to analyze the problem such as :-
- Settlement of foundations
- Stability (bearing Capacity) of foundations
- Stability of Slopes
- Stability of Retaining Structures
Types of Stresses
A soil mass is a skeleton of solid particles enclosing voids which contain water (saturated soil) or air (dry soil) or both (partially Saturated Soil), When stresses are applied, the volume of soil skeleton reduces due to rearrangement of soild particles into new positions, mainly by rolling and sliding.
The reduction in volume brings the particles closer resulting in an increase in the forces acting between the particles at the iner-particle contacts. The forces acting between the particles remain unchanged if the arrangement of the solid particles does not occur.
In a fully saturated soil, a reduction in volume is not possible, unless some of the water escapes from the voids. Water within the voids can also withstand stresses by an increase in pressure when the soil is fully saturated.
In a saturated soil mass, the following three types of stresses are generally considered while dealing with soil engineering problems :-
Total Stress
The stress developed at any point in a soil mass due to the total weight of the soil lying above that point is known as the total stress. It is the sum of the products of unit weight multiplied by thickness for all the layers above the level considered. If there is water above the ground surface it will also add to the total stress (unit weight of water x depth of water).
For the soil mass shown the total stress at Section X-X is written as follows :-
The expression for the total stress at section XX for the soil layers shown is as follow :-
Neutral Stress (Pore Water Pressure)
It is the pressure of water filling the voids between the solid particles. It is equal to the hydrostatic pressure (unit weight of water multiplied by the depth of water above the point where neutral stress is required).
It is termed as neutral stress since it acts equally in all directions.
It is important to keep in mind that the neutral stress reduces the inter-particle stress and this condition has an adverse effect on the strength of the soil.
The neutral stress or hydrostatic pressure at section XX is given by
Effective Stress
It is the portion of the total stress which is carried by the solid particles at their points of contact. In other words, it is the sum of the vertical components of the forces developed at the points of contact between the soil particles divided the cross-sectional area of the soil mass.
It is the effective stress due to which frictional resistance against particle movement such as rolling, slipping, sliding etc. develops.
If the effective stress is zero, the soil mass is in a critical (unstable) condition.
Effective stress is expressed as follow :-
The effective stress at section XX is therefore calculated as given below :-
γ_sub or γ_\’ is the submerged or buoyant unit weight of the soil.
If the water table rises to the ground surface the effective stress will be equal to “γ_sub (Z+D) and if the water table lowers down to XX, then the effective stress will be equal to “γ_b (Z+D)\”. Hence it can be said that the lowering of water table causes an increase in the effective stress, the effect of buoyancy is reduced.
Effective stress is independent of the depth of water above the ground surface.